에구 복잡해라... 저는 명색이 이과지만 수학은 손놓은지 오래라 무신 말씀을 하시는지 당최 모르겠군요.  그런데 위의 무차폐 반사망원경에 대해선 박병우님이 조금 오해하신 듯 합니다.  그런 식으로 만들어 가지곤 성능이 안 나오겠지요.

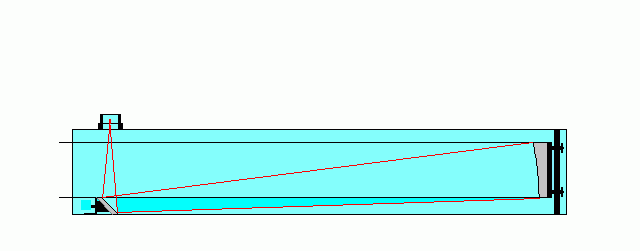
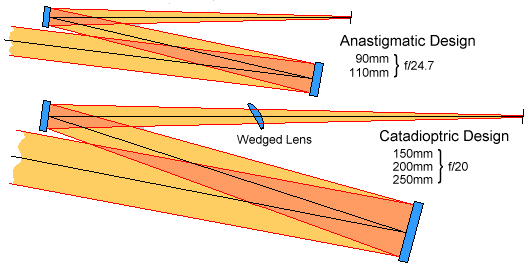
무차폐 반사망원경 중 제가 아는 것은 off-axis 뉴토니안 방식과 Schiefspiegler 방식이 있는데요, 각각의 구조는 위의 그림을 참고하시기 바랍니다.  자세한 것은 다음 링크를 참고하시구요.

Kutter Schiefspiegler 망원경을 생산하는 AOK Swiss 사의 홈 페이지
http://www.aokswiss.ch/e/english.html  

off-axis Newtonian 망원경을 생산하는 DGM Optics 사의 홈 페이지
http://users.erols.com/dgmoptics/







>망원경 차폐 형상에 따른 회절링의 광량 분포(1)
>
>이 글은 렌즈의 회절 이론을 숙지한 상태이고, 렌즈의 기본 물성치(굴절율, 분해능, 수차 등)을 이해한 분들을 대상으로 적습니다. 또 지난 번에 문병화씨와 차안에서 얘기했던 화제의 답변이기도 합니다만, 어디서부터 실마리를 풀어야될지, 내용을 추가, 보완해야될지, 또는 생략해야될지를 몰라서 일단 제가 생각한 순서대로 적습니다.  
>
>1. 무차폐 반사 망원경
>무차폐 반사 망원경을 아시나요? 여기서부터 얘기는 시작 됩니다. 문병화님의 이야기를 들어보면 아래와 같은 망원경을 무차폐 반사 망원경이라고 하는 것같습니다. 8인치 무차폐 반사 망원경을 제작하려면
><img src=http://www.qkrquddn.com/mpg/04050901.jpg>
>위의 그림처럼 18인치 F수 4의 미러를 가공합니다.
>
>초점길이 = 18인치 X 4 = 72인치(1828mm)
>
>인 미러가 완성될 것입니다. 이 미러를 제일 긴 끝단 길이가 8인치 정도 되도록 ‘쪼가리미러’로 자릅니다. 위의 그림은 설명의 편의를 위해 대충 그렸습니다만 실제로는 3쪼가리 정도가 나온다고합니다. 이 쪼가리미러의 원래 족보는 18인치였으므로 모든 물성치는 18인치의 지배를 받게 됩니다. 따러서 부경의 중심도 18인치 미러 중심이 될 것입니다. 이 미러를 가지고 반사망원경을 만든다면 부경은 18인치 중심에 있게 되고, 미러는 쪼가리가 되었으므로 부경 옆으로 쳐지게 위치해야됩니다. 이러면 부경의 차폐가 없는 8인치 초점거리 1828mm의 ‘무차폐 반사 망원경’이 되는 것입니다.
>
>눈감고 아옹하는 격이지만 무차폐인 것은 맞고 실제로 이렇게 생산하는 메이커도 있다는군요. 그렇다면 이런 제품을 왜 생산할까요? 여기서 의문은 시작되었습니다.
>
>1)18인치 하나 만들어 잘 자르면 8인치 무차폐 미러를 4개(or 3개)나 만들 수 있으므로 코스트면에서 유리하다? --->이건 장담을 못하겠습니다.
>2)아마도 오리지날 8인치보다 시잉 영향을 덜 받을 것이다.--->이것도 과학적인 근거가 희박하다고 보여집니다.
>3)이 쪼가리 미러의 오리지날 족보는 18인치 미러이므로 18인치 대구경 만큼의 분해능향상 효과가 있을 것이므로 오리지날 8인치보다는 화질이 좋을 것이다.--->이건 좀 타당하게 들리기도 합니다.    
>
>만약 무차폐 8인치가 오리지날 8인치보다 분해능의 향상이 있더라도 회절링 광량분포를 따져보지 않으면 안됩니다. 무차폐 8인치라는 것은 18인치 미러를 모두 차폐하고 8인치만 면적만 남겨둔 형태이기 때문입니다. 차폐율이 50%를 훨씬 넘어버린데다 그 형태도 원형 차폐가 아니고 이상한 모양의 차폐입니다.  
>
>반사망원경에서 차폐율이 40%가 넘어가면 저해상도 영역의 콘트라스트는 급격히 떨어집니다. 콘트라스트는 회절상의 광량분포와 밀접한 관계가 있습니다. 18인치 쪼가리미러가 콘트라스트가 확 떨어지더라도 8인치 오리지날 미러 보다는 낫다? 즉 '썩어도 준치다'라는 뜻일까요?
>
>2. 차폐에 따른 회절링 광량 분포와 모양은?  
>차폐를 하더라도 동일 구경이라면 회절링의 크기(직경)은 변하지 않습니다. 그러나 상점 중심(에어리디스크)과 그 주변 밝은 회절링의 광량 분포는 변합니다. 각 회절링(제1, 2, 3... 극대 밝기값)에서의 광량밝기가 계산된다면 무차폐반사망원경의 성능도 추정될 수 있을 것입니다. 이것을 더 응용하면
>
>1)기존의 슈미트카세 11인치(or 14인치)을 강제로 차폐 칸막이로 막았을 때의 화질은 좋아질 것인가? 나빠 질것인가?
>2)차폐 형상(사각 차폐, 원형 차폐 등)에 따른 회절링 형상은 어떻게 될까?
>등도 추정해 볼 수 있습니다.  
>
>
>3. 회절링과 광량 분포의 이론식
>(1)프레넬-키르호프식
>광량분포의 이론식은 에너지개념으로 풀이한 것이므로 대단히 복잡합니다. 지난 2월 24일 ‘회원카페’란에 적었던 ‘Star Testing Astronomical Telescope'에 나오는 프레넬-키러호프식(Fresnel-Kirchhoff formular)가 기본 공식이 됩니다.
>
>*뉴턴: 빛의 입자설
>*호이겐스: 빛의 파동설
>*프레넬: 호이겐스의 이론에 ‘간섭’을 추가함
>*키르호프: 호이겐스-프레넬 이론의 수학적 기초식을 세움
><img src=http://www.qkrquddn.com/mpg/04050905.jpg>
>윗 식은 U(x', y')라는 중간함수를 말하는데 이 식에는 빛이 렌즈를 지나던 아니면 그냥 지나던 어떤 필드를 지날 때 가질 수 있는 모든 변수(variable)를 다 넣어줍니다. 렌즈 구경, 빛의 위상각도(phase), 여러 수차들, 호이겐스 회절식, 빛의 이동 각도 등입니다.
>*광원에서 나온 빛이 차폐판 A에 의해서 일부는 차폐되고 일부는 통과할 경우 경우임
><img src=http://www.qkrquddn.com/mpg/04022402.jpg>
>위식은 피사체의 한광원에서 나온 빛을 상면의 밝기로 수식화시킬 수 있다는 의미입니다.  이 식을 풀려면 시간이 ‘엄청나게(a great deal of time)’ 걸린다고 이 교재는 적고 있습니다. 이 식은 피사체의 선명한 광원이 망원경의 회절, 차폐, 수차에 의해서 어떻게 상면에서 희미한 디스크로 되는지를 이론적으로 알 수 있게 해주고 그 비율도 알 수 있게 해줍니다.
>
>(2)프라운호퍼회절(Fraunhoffer diffractiton) 회절과 프레넬회절(Fresnel diffractiton)
><img src=http://www.qkrquddn.com/mpg/04050902.jpg>
>*상면에서 맺어진 광파의 진폭을 U(p)라고 할 경우의 식이다.
>*실제로 상면에 나타나는 것은 빛의 강도이므로 ‘빛의 강도 = 절대값 진폭^2’이 된다.
>*e^ik(r+s) = e^2phi(r+s)/람다 함수는 r+s가 파장 람다만큼 변화는 하는 것으로 복소수평면상에서 원점을 한번 회전할 때의 주기함수이다.
>
>e^ik(r+s) = (cosik(r+s) + isin(ik(r+s))
>
>*r+s값은 람다의 몇천배 몇 만배나 회전할 것이므로 적분중에 이 함수는 -1과 1 사이를 몇천번 몇만번이나 진동하는 것이 된다(r+s의 값이 파장 람다만큼 변하는 것이 되므로 +1-->-1-->+1로 1회 진동) 따라서 이 식을 수치적분하면 계산 방법을 이 사항을 충분히 고려하지 않으면 계산 결과가 오차에 묻혀버린다. 이 것을 회피하기 위한 방법으로 r, s를 급수전개한다.
><img src=http://www.qkrquddn.com/mpg/04050903.jpg>
>*위의 식은 아직 렌즈가 고려되지 않은 일반 개구부임
>
>여기서 천체망원경의 경우는
><img src=http://www.qkrquddn.com/mpg/04050904.jpg>
>*(B-6)식이 천체망원경의 초점면에서의 회절식이다.
>
>개구부 형상(차폐)에 따른 윗 식 방식의 계산 예는 다음에 적겠습니다.
>To be continued....
>
>