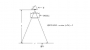
뉴튼식 반사망원경에서 옵셋(이격거리)의 개념은 망원경의 광학적인 광축과는 관계없으며, 옵셋은 그 목표를 어떻게 설정하느냐에 따라 구하는 공식이 달라지게 됩니다.
옵셋의 목표를 두 가지만 예시해 보겠습니다.
첫 번째 목표는, 아이피스 없이 초점면에 눈을 위치했을 때 보이는 사경과, 사경을 통해 보이는 주경이 동심원을 이루도록 옵셋의 목표를 설정하는 것입니다.
두 번째 목표를 설명하기 위해서, 예를 들어 망원경을 수직으로 세워서 천정에 있는 별을 관측한다고 했을 때, 제가 아래 글에서 제시했던 100% 조명범위는 수평방향의 100% 조명범위를 유도한 것입니다. 엄밀하게 말해서 100% 조명범위는 정확한 원이 아니기 때문에 수직방향의 100% 조명범위는 수평범위의 그것과 약간의 차이를 보이게 되는데요, 제가 제시하는 옵셋의 두 번째 목표는 수직방향의 100% 조명범위의 중심이 접안부의 중심과 일치하도록 옵셋의 목표를 설정하는 것입니다.
위 두 가지 목표는 서로 다르기 때문에 공식도 다르고 옵셋의 양도 아주 작은 차이를 보일 것으로 예상되는데요, 제 생각에는 두 번째 목표가 더 적합한 것으로 판단합니다. 특히 천체사진을 찍으시는 분들은 두 번째 목표로 옵셋을 설정하게 되면, 그 망원경의 100% 조명범위의 중심이 ccd 면의 중심과 일치하게 되기 때문에 두 번째 목표를 더 선호하게 될 것으로 봅니다.
(하지만 두 옵셋의 크기는 그 차이가 실제적으로는 아주 작기 때문에 그 차이는 무시해도 좋을 것 같습니다)
그래서 옵셋의 목표를 두 번째로 잡고 필요한 옵셋의 크기를 유도해 봤는데요, 유도과정은 복잡하지만 그 결과는 다음과 같이 비교적 간단한 공식으로 나왔습니다.
옵셋의 크기(mm) = [a - root of {a*a-(D-d)*d}] / 2
여기에서,
a = 주경중심에서 사경까지의 거리 (mm) (즉, 아래 글에서는 a = f-b 입니다)
D = 주경 크기 (mm)
d = 사경의 단경 (mm)
※ 만일 사경에 옵셋 포인트를 표시하시려면 사경의 중심에서 위 방향으로
(옵셋의 크기) * (root of 2)
만큼 떨어진 곳에 표시하시면 됩니다.
또한, 이 옵셋을 적용했을 때 접안부 초점위치에서 수직방향의 100% 조명범위는 다음과 같이 유도되었습니다.
수직방향 100% 조명범위(mm) = D -4*f*(옵셋의 크기)/d
여기에서 f는 물론 주경의 초점거리입니다.
제 망원경 HP250으로 예를 들어 보겠습니다.
d=56mm (차폐율 22%)
D=250mm
f=1520mm
a=1313mm
이므로 이를 공식에 적용해서
옵셋의 크기 = 2.072mm
가 나왔으며, 이 옵셋을 적용할 경우
수직방향 100% 조명범위 = 25.04mm
로 계산되었습니다. 아래의 글에서 계산한 수평방향의 100% 조명범위 25.4mm 보다는 약간 작게 나오는군요.
옵셋의 목표를 두 가지만 예시해 보겠습니다.
첫 번째 목표는, 아이피스 없이 초점면에 눈을 위치했을 때 보이는 사경과, 사경을 통해 보이는 주경이 동심원을 이루도록 옵셋의 목표를 설정하는 것입니다.
두 번째 목표를 설명하기 위해서, 예를 들어 망원경을 수직으로 세워서 천정에 있는 별을 관측한다고 했을 때, 제가 아래 글에서 제시했던 100% 조명범위는 수평방향의 100% 조명범위를 유도한 것입니다. 엄밀하게 말해서 100% 조명범위는 정확한 원이 아니기 때문에 수직방향의 100% 조명범위는 수평범위의 그것과 약간의 차이를 보이게 되는데요, 제가 제시하는 옵셋의 두 번째 목표는 수직방향의 100% 조명범위의 중심이 접안부의 중심과 일치하도록 옵셋의 목표를 설정하는 것입니다.
위 두 가지 목표는 서로 다르기 때문에 공식도 다르고 옵셋의 양도 아주 작은 차이를 보일 것으로 예상되는데요, 제 생각에는 두 번째 목표가 더 적합한 것으로 판단합니다. 특히 천체사진을 찍으시는 분들은 두 번째 목표로 옵셋을 설정하게 되면, 그 망원경의 100% 조명범위의 중심이 ccd 면의 중심과 일치하게 되기 때문에 두 번째 목표를 더 선호하게 될 것으로 봅니다.
(하지만 두 옵셋의 크기는 그 차이가 실제적으로는 아주 작기 때문에 그 차이는 무시해도 좋을 것 같습니다)
그래서 옵셋의 목표를 두 번째로 잡고 필요한 옵셋의 크기를 유도해 봤는데요, 유도과정은 복잡하지만 그 결과는 다음과 같이 비교적 간단한 공식으로 나왔습니다.
옵셋의 크기(mm) = [a - root of {a*a-(D-d)*d}] / 2
여기에서,
a = 주경중심에서 사경까지의 거리 (mm) (즉, 아래 글에서는 a = f-b 입니다)
D = 주경 크기 (mm)
d = 사경의 단경 (mm)
※ 만일 사경에 옵셋 포인트를 표시하시려면 사경의 중심에서 위 방향으로
(옵셋의 크기) * (root of 2)
만큼 떨어진 곳에 표시하시면 됩니다.
또한, 이 옵셋을 적용했을 때 접안부 초점위치에서 수직방향의 100% 조명범위는 다음과 같이 유도되었습니다.
수직방향 100% 조명범위(mm) = D -4*f*(옵셋의 크기)/d
여기에서 f는 물론 주경의 초점거리입니다.
제 망원경 HP250으로 예를 들어 보겠습니다.
d=56mm (차폐율 22%)
D=250mm
f=1520mm
a=1313mm
이므로 이를 공식에 적용해서
옵셋의 크기 = 2.072mm
가 나왔으며, 이 옵셋을 적용할 경우
수직방향 100% 조명범위 = 25.04mm
로 계산되었습니다. 아래의 글에서 계산한 수평방향의 100% 조명범위 25.4mm 보다는 약간 작게 나오는군요.
 굴절망원경 론키상 테스트 리스트
굴절망원경 론키상 테스트 리스트