이윤씨 그림 그려서 설명하시느라 대단히 수고하셨습니다만 아쉽게도 이해를 못하는 것도 있고 납득이 힘든 것도 있습니다. 설명드리겠습니다.
1. 빛의밝기(intensity)와 광량
이 개념부터 제 생각을 먼저 적겠습니다. ‘빛의 밝기’와 ‘광량’은 다르다고 생각합니다. 빛의 밝기는 ‘빛의 강도(intensity)'를 말하고 광량은 '에너지'를 말한다고 생각하지요. 즉 밝기가 세면 빛 에너지가 많아지는 것은 맞지만 반드시 비례하지는 않다고 생각합니다.
.
다른 자연계와 마찬가지로 빛도 밝기(강도)를 분포 곡선에 대해 적분을 해주거나 하면 광량(에너지)이 된다고 생각합니다. 이 혼동이 지난번에도 있었는데 1/4람다 미러에서 에어리디스크의 최대빛의 밝기는 무수차의 미러의 80%(?)정도이다라고 한 기억이 있습니다. 그러나 다른 교재에서는 광량(에너지) 기준으로 60%(?)로 수치를 달리 표기를 하는 모양이었습니다. 이 수치 차이가 밝기와 광량 차이라고 생각을 하지요. 즉 밝기(피크치)가 적더라도 에어리디스크 면적이 커지면 광량은 동일하게 나올 수가 있다고 생각합니다.
2. 인간의 눈은 밝기(강도)에 따른 인식인가 광량(에너지)에 따른 인식인가?
인간의 눈은 잘 모르겠습니다만 필름이나 CCD는 모두 광량(에너지) 기준입니다. 자연계에서는 통상 에너지기준으로 계산을 합니다. 그러나 인간의 눈은 과연 밝기인지 광량인지를 모르겠군요. 일단 광량이 별 식별 기준이라고 보고 적겠습니다. 이윤씨의 계산도 그렇게 보고 했군요.
3. 구경 100mm F4(A망원경)과 구경 100mm, F10(B망원경)의 광량 차이
구경이 같으면 입사 되는 광량(에너지)는 F수에 관계없이 같다고 생각합니다. 이윤씨 계산에서 구경의 반경제곱을 광량항목으로 대치했는데 이것은 상대비교에서 별 문제가 없다고 생각합니다. 이윤씨의 계산된 결과치는 엄밀하게 말하면 동공의 단위 면적당에 비치는 광량이라고 하면 무방하겠습니다. 이 말을 적은 이유는 구경이 같더라도 F수가 다르면 광량이 다르구나라는 오해를 하는 분들이 계실까봐 적었습니다.
4. 그럼 이윤씨의 계산은 무엇을 의미할까요?
이윤씨의 명시거리 200mm점에서의 밝기 계산은 무한원의 광축상의 별빛(예 달만큼 밝은 점상별이 있다고합시다)이 들어왔을 때, 그 위치에서 간유리를 대었을 때 밝기 분포라고 생각합니다. 즉 F4는 스크린 면적이 크므로 전반적으로 어둡고 F10은 면적이 작고 밝게 보입니다. 이것을 동공에 대비하여 나누어서 그 면적비를 보고 있습니다. 이것은 A, B 망원경의 F수에 따른 인간의 동공과 얼마나 면적차이가 나는 것을 보고 있지요. 스크린면적이 동공보다 더 크면 광량 손실이 일어난다고 말하고 있습니다.
5. 스크린 면적과 동공의 관계
극단적으로 만약 인간 동공의 크기가 A 망원경 F4 크기 스크린면의 크기라면 광량 손실이 없으므로 A 망원경도 구경 100mm 광량을 충분히 이용할 수 있습니다. 단지 명시거리의 변화가 있겠지요. 여기서는 명시거리를 200mm로 고정했으므로, F4인 망원경에서 200mm 지점에서 스크린면의 크기는 50mm나 되어 동공 7mm보다 훨씬 큽니다. 과연 이렇게 되면 어떻게 될까요?
6. 실제로 보았을 때
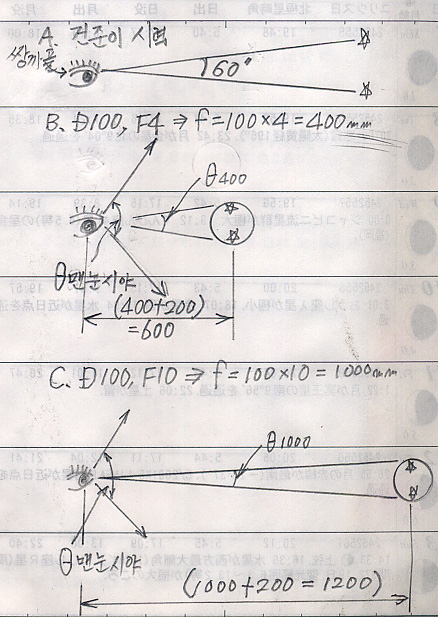
1)조리개(튜브)가 없을 때
위의 그림처럼 A, B 망원경의 튜브를 삭제하고 돋보기만 두었을 때 입니다. 건준이 눈에 들어오는 광량은 ‘세타맨눈시야’는 일정이므로 광량은 같습니다. 단지 A망원경은 돋보기가 가까이 있어 시야각을 많이 가립니다(세타400이 크다). 이것은 건준이 눈 입장에서 보면 돋보기가 차지하는 광량면적이 크게 되어 건준이 눈에는 돋보기 투과 광량이 많은 비율을 차지합니다. B망원경은 스크린면적은 줄어들지만 시야각(세타1000)이 적어서 A망원경보다, 건준이 눈에 투과되는 광량비율이 적습니다. 즉 A, B 돋보기자체의 광량도 같고, 위치에도 따라서 건준이 눈이 인식하는 광량도 결국 같아지지 않을까요? 여기서는 스크린의 밝기 차이가 건준이가 인식하는 별구별 능력에 차이를 주지 않는다고 생각합니다.
2)조리개(튜브)를 건준이 눈까지 연장하고 잡광을 차단했을 때
이럴 경우는 오직 돋보기로 통하는 광량뿐입니다. 이 문제의 답은 이럴 경우 B망원경(F10)이 밝게 보인다는 이야기인데요. 제 3자가 건준이 눈 부분을 보았을 때 A망원경은 어둡게 넓게 비치고, B망원경은 밝고 좁게 건준이 눈동공을 비치리라 생각합니다. 이건 이 위치에 간유리를 비쳤을 때 비치는 밝기와 같다고 생각합니다. 그러나 건준이가 느끼는 별의 인식은 그렇지 않다는 생각입니다. 건준이가 보는 도립실상 위치는 초점면에 보이는 것이 아니고 렌즈 뒷면에 맺히는 것처럼 보이기 때문입니다. 실제 돋보기를 보면 렌즈 뒷면에 렌즈구경크기만큼의 도립실상이 맺혀있는 것처럼 보입니다. B망원경의 경우는 렌즈의 거리가 멀어 먼 위치에서 별이 보이는 것과 같습니다. 결국 밝게 보이더라도 거리만큼 밝기 감소치가 존재하게 되어 실제로 보았을 때는 구경이 같으면 별식별 능력은 같지않을까 생각합니다. 또 눈으로 보았을 때는 거리가 멀고 가까움에 따라 화각이 변동되어 자동적으로 밝기가 같아지는 것은 아닐까요? 이건 필름이라면 그렇지 않겠지만 우리 눈의 작용으로 그렇게 되지않을까요. 참 알쏭달쏭하군요.
ps) 이 원리에서 본다면 두별간의 식별 능력을 말하는 5번은 답이 아님을 알 수 있습니다. 건준이 눈과 돋보기 거리를 고려해야하니까요.

 [re] [광학퀴즈] 다함께 풀어봅시다.
[re] [광학퀴즈] 다함께 풀어봅시다.
 [re] [광학퀴즈] 다함께 풀어봅시다.
[re] [광학퀴즈] 다함께 풀어봅시다.









.
이럴 경우는 오직 돋보기로 통하는 광량뿐입니다. 이 문제의 답은 이럴 경우 B망원경(F10)이 밝게 보인다는 이야기인데요. 제 3자가 건준이 눈 부분을 보았을 때 A망원경은 어둡게 넓게 비치고, B망원경은 밝고 좁게 건준이 눈동공을 비치리라 생각합니다.
-->이 설명은 광축상에 무한원에서 달만큼 밝은 점광원이 있다는 가정이고 그 위 부분은 광량이 전혀 없는 경우입니다. 만약 그 외 부분에도 광량이 있다면 스크린면의 크기는 장초점이 커지겠지요.