[퀴즈풀이]

(퀴즈 풀이)
(지루하시더라도 이 풀이를 자세하게 읽으시면 망원경의 에어리디스크를 이해하시는데 도움이 될 것으로 생각합니다)

먼저, 필름면에서의 "각거리"와 "거리"(또는 "길이")라는 용어를 분명하게 구분해서 씁시다.
잘 아시겠지만 "각거리"는 1초각, 2초각, 또는 0.05라디안 등처럼 쓰는 것이고 "거리"는 1mm, 2mm 등으로 쓰는 것입니다. 필름면에서 두 점 사이의 "각거리"와 "거리"의 관계는 다음과 같습니다.

[사실1]   (거리) = (광학계의 초점거리) * (각거리)
        (단, 각거리의 단위가 라디안이라고 가정할 때입니다.)

에어리디스크의 "각직경"은 지름의 "각거리"이고, 그 광학계의 각분해능(우리가 보통 말하는 분해능임)을 결정합니다. 각분해능이 좋으면 많은 것을 자세하게 보여줄 수 있습니다.
에어리디스크의 "직경"은 지름의 "거리"이고, 그 광학계의 선분해능을 결정합니다. 선분해능이 좋으면 깨알같이 보여주긴 하지만, 그건 동일구경 대비 초점거리가 짧아져서 배율이 낮아진 효과일 뿐 많은 것을 자세하게 보여주는 것은 아닙니다.

[사실2]  (빛의 파장이 일정할 경우 무차폐 광학계에서) 에어리디스크의 "각직경"은 그 망원경의 구경에 반비례합니다(이 부분을 이해하려면 회절의 원리를 어느정도는 이해해야 합니다). 즉, 구경이 2배 커지면 에어리디스크의 각직경은 1/2로 (예를 들어 2초각에서 1초각으로) 줄어들게 되어 각분해능이 2배 좋아진다고 말합니다.

[사실3] (빛의 파장이 일정할 경우 무차폐 광학계에서) 에어리디스크의 "직경"(지름의 거리)은 구경에 관계없이 F수에만 비례합니다. 즉, F수가 1/2로 짧아지면 에어리디스크의 직경도 1/2로 작아집니다. 왜냐하면, [사실1]에서
          (직경) = (광학계의 초점거리) * (각직경)  
인데 [사실2]에서 (각직경)=(상수)/(구경) 이므로 이를 위식에 대입하면
       (직경) = (광학계의 초점거리) * (상수) / (구경) =(상수) * (F수)
이기 때문입니다.
  
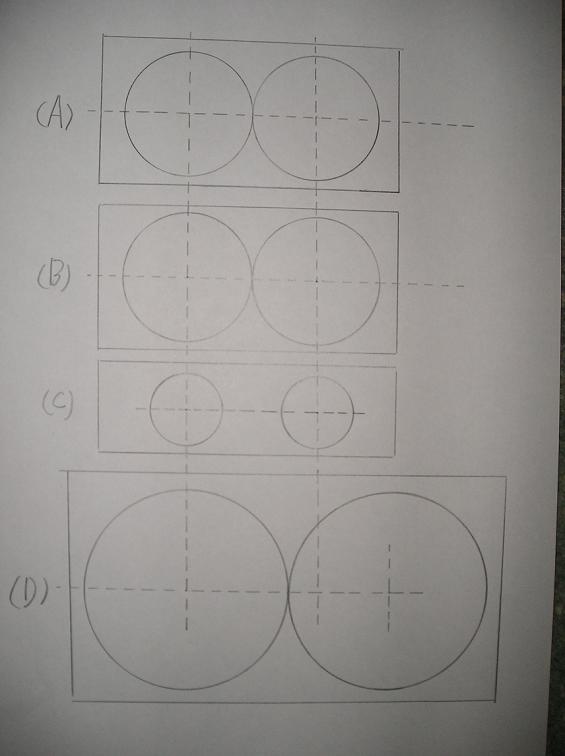
이제 문제의 그림을 봅시다.

(1)의 해설:
두 에어리디스크의 중심간의 "각거리"는 관측한 이중성의 각거리이므로 고정입니다.
따라서 망원경 A, B, D에서는 두 원들이 모두 접하고 있어서, 에어리디스크의 "각직경"은  모두 관측한 이중성의 "각거리"와 일치하므로 망원경 A, B, D의 에어리디스크의 "각직경"은 모두 같습니다.
그렇다면 B와 D는 모두 무차폐 광학계이므로 [사실2]에 의하여 같은 구경을 갖습니다.
또한, 앞의 힌트에서 차폐망원경의 에어리디스크의 각거리는 동일구경의 무차폐망원경보다 약간 작아진다고 했는데(이 부분을 이해하려면 회절의 원리를 어느 정도는 이해해야 합니다), 이를 적용하면, A는 차폐광학계인데 B, D와 같은 각직경의 에어리디스크를 갖고 있으므로 구경은 약간 더 작습니다. (구경이 같다면 차폐광학계에서의 에어리디스크의 각직경은 약간 더 작은 값을 갖는데, 거기에 구경이 더 커진다면 각직경은 더 작아질 것이므로 각직경이 같을 수가 없겠지요.)
C는 에어리디스크의 각직경이 현저하게 작으므로 [사실2]에 의하여 가장 큰 구경입니다.
결론적으로 (1)의 답은 A<D=B<C입니다.

(2)의 해설:
위의 [사실3]에서 (무차폐 광학계에서) 에어리디스크의 "직경"은 구경에 관계없이 F수에만 비례한다고 하였으므로, 무차폐광학계인 B, C, D에서 F수의 크기순서는 C<B<D입니다. 즉, (1)에서 B와 D는 구경이 같은데 D가 크게 찍혔다는 것은 D의 초점거리가 길다는 뜻이고 따라서 B보다 큰 F수를 갖는 것입니다.
또한 A, B, C 에서의 이중성의 중심간의 "거리'가 같다는 것은, 세 망원경의 초점거리가 같다는 걸 의미합니다. 따라서 이들의 F수의 크기 순서는 구경의 역순이므로 C<B<A입니다.
이제 A와 D의 F수의 크기비교가 남았는데, 힌트에서처럼 초점거리가 같은 A와 B의 구경크기는 6.4% 차이인데 비하여, 구경이 같은 B와 D의 초점거리의 차이는 그림에서 적어도 20% 이상의 차이를 보이고 있으므로, A<D 입니다.
결론적으로 (2)번의 답은 C<B<A<D 입니다.