김청님의 생각에 몇가지 착오가 있습니다. 누구나 생각하기 쉬운 착오입니다.
1. 분해능
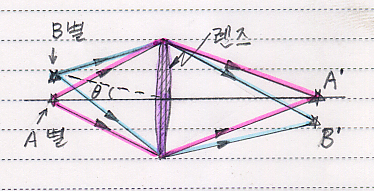
위의 그림을 봅시다. A, B별이 볼록렌즈를 지나서 A', B' 점에 초점을 맺는다고 생각합시다. 여기서 왜 A', B‘점에 초점이 맺히는가를 생각해보는 것이 시작입니다.
일단 A가 A'에 맺히는 경우를 먼저 생각해봅니다. 점광원 A가 렌즈를 지나서 A'로 오기까지 3가지 광로만 우선 생각해봅니다.
1) A-->렌즈 상단-->A'
2) A-->렌즈 중앙-->A'
3) A-->렌즈 하단-->A'
여기서 빛이 오는 거리가 가장 가까운 코스는 2)번이고 1), 3)번은 가장 먼 길(광로)를 돌아서 오는 경우입니다. 렌즈를 통하여 1), 3)번보다 더 먼 광로는 없습니다. 그럼 빛 A가 A'에 올 때까지의 걸리는 시간을 생각해봅시다. 걸리는 시간은 1), 2), 3)번 모두 똑 같은 시간에 A'에 도달합니다. 1), 3)번은 상하대칭이므로 시간이 같이 걸리는 것은 쉽게 짐작할 수있습니다. 1)번의 경우는 거리는 짧지만 중간에 두꺼운 렌즈유리를 지나야합니다. 렌즈 중앙부는 렌즈 두께가 제일 두꺼우므로 그만큼 빛의 속도는 느려지게 됩니다. 즉
* 필름면에 별빛이 맺히는 점(초점)은 피사체 점광원의 빛이 렌즈로 통하여 도착하는 시간이 같은 지점이다.
라고 말할 수 있습니다. 그 다음 A별과 세타 각도 떨어진 B별의 상 맺힘을 생각해봅니다. 이 때 세타각도는 렌즈로 입사되는 A, B별의 각도입니다. B별은 B'에 맺히게 되는데, 역시 위의 경우와 마찬가지로 1). 2). 3) 코스로 오는 빛의 시간이 같은 지점입니다. 만약 B별이 A'에 맺힌다면 도착 시간이 달라서 빛이 동시에 모일 수가 없습니다. 그러므로 A점에 상이 맺히지 않습니다.
여기서 만약 A, B 별이 아주 아주 가까이 있는 경우입니다(세타가 아주 아주 작을 경우). 이럴 경우 B별의 1). 2). 3) 코스는 A별과 코스와 거의 같으므로 A'지점에 A, B 별이 같은 위치에서 상이 맺힐 것입니다. 즉 A, B 두 별을 분리하여 상을 맺을 수 없습니다. 이럴 경우 두 별을 분리하여 상을 맺으려면 렌즈의 구경을 키워서 코스 길이 차이를 크게 하면 됩니다. 구경을 키우면 코스마다 시간차가 나게 되고 아주아주 작은 각도 떨어져도 두 별은 분리되어 분리된 상을 맺어줄 것입니다. 이를 렌즈의 분해능이라고 합니다. 즉
*두 별이 분리되어 맺히려면 그 렌즈의 구경에서 1), 3) 코스로 오는 별빛의 시간차가 빛의 한주기 시간차가 날 정도로 떨어져 있을 경우이다. 이 각도를 분해능이라고 한다.
*렌즈의 분해능은 ‘오직’ 렌즈의 구경(김청민씨 얘기대로 가장자리)과 매질의 굴절율에만 의존한다.
*렌즈의 구경이 크면 아주 아주 가까운 두별을 쉽게 구별해줄 수있다...= 분리할 수 있는 각도가 작다. = 분해능이 좋다.
*렌즈의 구경이 작으면 아주 아주 가까운 두별을 쉽게 구별해줄 수 없고 한점에 모여 빛난다...= 분리할 수 있는 각도가 크다. = 분해능이 나쁘다.
로 말할 수 있습니다. 김청민의 60mm 굴절은 분해능이 대략 2초 정도이고 구경이 150mm 망원경은 0.77초가 됩니다.
2. 회절과 레이리 원반
윗 그림에서 광축상의 별 A가 A‘에 맺히는 경우를 생각합니다. A 광량의 100%가 A'에 맺힐 수는 없지요. 그 이유는 빛의 회절과 간섭 때문입니다. 99%(?) 이상의 광량은 A' 점에 맺히나 나머지는 회절과 간섭에 의해서 A'점 외측으로 퍼져나갑니다. 이 때 A'점의 빛 원반 크기를 ’에어리디스크‘ 또는 ’레일리 원반‘이라고 합니다. 그런데 A, B 두별이 구별이 되기 위해서는 레일리원반의 반경 정도만 떨어져 맺혀도 사람은 구별할 수 있습니다. 이것은 위에서 말한 한주기 시간차 계산과도 일치합니다. 그 상세 설명은 생략합니다. 즉
*분해능 각도 ≒ 레일리원반의 반경 각도
가 됩니다.
...........................................
이상 서두 설명을 끝내고 김청민님의 궁금증에 바로 답을 하겠습니다.
[회절이 되는 것은 렌즈에 입사되는 광자들 중에서 렌즈의 가장자리에
입사하는 것들 뿐이고 그것들이 망막(필름)에 레일리 원반을 만들더라도
렌즈 중심쪽으로 들어오는 광자들은 정확한 상을 만들 것임.]
--->렌즈의 가장자리 크기(구경 크기)는 두 별이 분리 되는 최소 각도를 결정해주고, 레일리원반의 크기를 결정해줍니다. 그 때 렌즈의 가장자리 안쪽에서 들어오는 광선들은 레이리 원반의 밝기를 더 밝게 해줍니다. 만약 렌즈 가장 자리만 남겨두고 안족 부위의 99%를 차폐를 했을 경우에도 그 렌즈의 분해능은 변하지 않으며, 레일리 원반 크기도 변하지 않습니다. 다만 상점(像点)에서의 광량만 변합니다. 물론 상점의 광량 강도 분포의 위치도 변하지않습니다.
[렌즈 지름이 증가함에 따라 가장자리 길이는 지름에 비례해 증가하지만
렌즈전체 면적은 지름의 제곱에 비례하므로 결국 렌즈 지름이 어느 정도
커지게 되면 회절에 의한 방해 영상은 점점 그 비율이 작아지게 됨.
그렇다면 회절로 인한 배율 제한 (분해능 제한)은 렌즈크기가 좀 커지면
맞지 않는 이론이 되어버리고, 실제로는 렌즈를 잘만 만들면 60mm 같은
소구경 렌즈로도 고배율(대기 공기 제한치 이내)이 가능하다?]
--->분해능은 구경에 의해 결정되는 것은 앞에서 설명한대로이고, ‘회절로 인한 배율 제한’이란 말은 국산책이 애매하게 번역해서 그렇습니다. 요건 아래의 유효 배율에서 설명하겠습니다. 그러므로 60mm를 아무리 고배율로 해도 분해능의 한계치인 2초각 이상을 분해할 수 없습니다. 고배율은 할 수 있겠지만 해 봤자 그 이상의 정보량은 얻을 수 없습니다.
................................
(참고 설명)
유효 배율
어떤 시력을 가진 사람이 그 망원경의 분해능까지 볼 수 있는 배율을 유효 배율이라합니다.
사람의 시력은 랜들씨 환(環)이란게 있는데, 이 눈금의 1분각을 분해하면 시력 1.0이라고하고 30초를 분리하면 2.0이라 정의합니다. 1.5는 45초각이 되겠지요.
그렇다면 시력 1.0인 사람이 망원경을 본다면 유효 배율은 1분각(60초)을 그 망원경의 분해능으로 나누어주면 되겠지요. 이렇게 되면 그 사람이 자기 시력으로 그 망원경의 분해능까지 볼 수 있는 배율이 됩니다. 즉
유효배율 = 60초/(분해능x시력)이 됩니다.
이것을 고려하여 계산하면 150mm 망원경의 경우 시력 1.2인 사람이 본다면
유효 배율 = 60초각/(0.77초각x1,2시력) = 65배
시력 1.0인 사람은...78배
이 배율이면 6인치 굴절의 분해능 한계까지 다 볼 수있습니다. 그런데 이 값에서 2배를 곱하면 ‘유효 최고 배율’이되고 이 값을 기준으로 합니다. 이렇게 올린다고 이론적으로는 더 보이는 것은 없고 그냥 시원하게 보이는 것 밖에 없습니다. 실제로 망원경이 아닌 측량기는 이 두 배값을 유효배율로 하고 있습니다.



