>반사망원경에 대 해 질문입니다.
>어느 망원경이든 옵셋은 존재한다고 했읍니다.
>그 간격은 얼마인지 알고 싶고요, 옵셋은 어느방향으로 움직여야
>하는지 알고 싶습니다. 접안부에서 반대쪽으로 밀어야 하는지 아니면
>주경쪽으로 밀어야 하는지... ^_^
>답변 부탁드리겠읍니다.
우선, 옵셋이란 광축조정과는 아무런 관련이 없다는 점을 이해하셔야 합니다.
단지 옵셋이란 사경의 크기가 넉넉하지 않을 때 사경을 가장 효율적으로 이용하기 위하여 그 위치를 최적화하는 것이며, 만일 사경의 크기가 충분히 크다면 옵셋은 고려할 필요가 없습니다.
그렇다면 옵셋을 고려할 필요가 없게 아예 사경의 단경이 주경의 직경에 맞먹을 정도로 큰 경우를 가상으로 가정해 봅시다. 이 때, 광축이 정확한 상태는 오직 유일하게 존재하는데 다음과 같습니다.
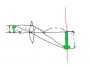
우선 주경의 중심축과 접안부의 중심축이 반드시 교차하도록 주경, 또는 접안부를 먼저 조정해야 합니다. (이 두 축이 교차하지 않은 상태에서 이상적으로 정확한 광축 조정은 존재하지 않습니다. 다만 꼭 직각으로 교차할 필요는 없습니다. 그러나 직각으로 교차하면 초점면과 사경의 거리가 최소화되어 유리합니다.) 공간상의 그 교점을 A라고 합시다. 정확하게 광축을 조정하려면 우선 사경의 반사평면이 반드시 점A를 지나도록 위치시켜야 합니다. 자, 이제 사경의 반사평면의 어떤 한 점 B가 점A에서 떨어지지 못하도록 가상의 못 하나를 공간에 박아 두 점이 떨어지지 못하도록 합시다. 그렇게 하더라도 마치 칭동과 같이 아직 사경은 전후좌우로 움직일 수 있습니다. 다만 점B는 점A에 묶인 채로...
이제 사경을 점B가 점A에 묶인 채로 전후좌우로 움직여 정확한 광축이 되도록 하는 사경의 위치는 유일하게 존재합니다. 그것은 주경중심축이 사경에 의해서 반사된 연장선이 접안부의 중심축과 일치하도록 하는 사경의 위치입니다. 그렇게 되면 광축조정은 완벽하게 끝난 것이며, 이제까지 옵셋은 전혀 관계없다는 것을 알았을 것입니다.
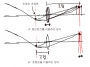
이제 사경의 크기가 너무 크므로 광축이 정확한 상태에서 사경을 적당한 크기의 타원으로 잘라내기로 했다고 합시다. 타원에는 두 개의 초점이 있는데 두 초점의 중심을 그 타원의 중심이라 하고 점C라고 합시다. 이때 사경의 사용효율을 극대화하기 위해서는 점C와 점B가 일치하여야 할까요? 그렇지 않다는 것입니다! 간단한 광로도만 그려보면 쉽게 이해가 될 것입니다. 그림그리기가 귀찮으므로 각자 생각해보기로 하고...
사경의 사용효율을 극대화하기 위해서는 타원사경의 중심 C가 점B 보다 접안부에서 멀고 주경에 가까운 위치가 되도록 사경을 잘라내야 합니다. 이를 옵셋조정이라고 하고, 점B와 점C 사이의 거리를 2의 제곱근(루트2)로 나눈 양을 옵셋이라고 합니다.
다시 강조하지만, 옵셋은 광축과는 관계없으며, 사경의 크기가 넉넉할 때는 굳이 옵셋을 고려할 필요가 없습니다. 광축이 맞은 상태에서는 사경의 연장평면상에서 사경을 슬라이딩시키더라도 광축은 맞은 상태인데, 사경의 사용효율이 극대화되는 위치로 사경을 접안부에서 멀고 주경에 가까워지게 45도 각도로 슬라이딩시키는 것을 옵셋조정이라고 하는 것입니다.
옵셋까지 조정한 후에 접안부의 초점위치에 체사이어를 장치하고 보면 어떻게 보여야 할까요? 보이는 순서는 다음과 같을 것입니다.
1) 접안부의 끝부분(원형1)
2) 사경(원형2)
3) 주경(원형3) 및 주경의 센터마크(원형4)
4) 주경에 비친 사경(원형5)
5) 주경에 비친 사경 속의 체사이어의 중심(원형6)
이 중에서 원형5를 제외한 원형1, 2, 3, 4, 6은 모두 동심원을 이루어야 하며, 원형5는 약간 접안부 반대쪽으로 위치하게 되지만, 일반적으로 F수가 아주 짧은 경우가 아니면 그 차이가 너무 적어서 거의 동심원으로 보이게 되는 것입니다.