제 이름이 들어가 있어 경면정밀도에 대해서 보조 설명합니다.
경면정밀도는 과거 미러 가공시의 경면정밀도 내용을 정리한 내용을 말하는 것같습니다. 이 내용은 적은지가 오래되서 잘 기억이 안납니다만 틀린 내용은 없을겁니다. 왜냐하면 교재를 그대로 베꼈으므로.-_-‘’
단지 파면오차(wave front error)의 개념에 대해서 추가 설명을 하고자합니다. 우리가 통상 이야기하는 1/4람다냐 또는 1/8람다냐하는 것은 파면오차(or 파면수차)를 말합니다. 여기에 대해 별친구들의 인식이 차이가 있는 것같은데 제가 생각하고 있는 파면오차는 다음과 같습니다.
만약 미러가 이론적으로 완벽한 미러라면, 미러에서 반사된 빛다발은 초점면의 한점으로 수렴을 할 것입니다. 빛은 파동이므로 미러에서 반사 회절되어 상점(像点)을 향해서 동심 구면(球面)으로 진행되어 옵니다. 결국은 초점면에서 에어리디스크라는 작은 원반을 만들게 됩니다. 이 파면은 빛의 산부분을 연결하는 파로 진행하는데 파장이 크면 에어리디스크원반도 크게 됩니다(이것은 물리책 호이겐스 원리에 의한 굴절편을 참조하세요).
그런데 미러가 완벽하지 않고 울퉁불퉁하다면 이 파면도 동심구면이 아닌 울퉁불퉁하게 진행되어 올 것입니다. 이 때 에어리디스면도 둥근원이 아닌 울퉁불퉁하게 되어 보일 것입니다. 이 때 원래 에어리디스크(참조구면)보다 제일 오차가 발생한 파면과 에어리디스크의 기준면 차이를 PV오차라고 합니다. 이 기준면 차이를 평균하고 평균과의 차이를 제곱하여 표준편차로 나타낸 것을 RMS 오차라고 합니다.
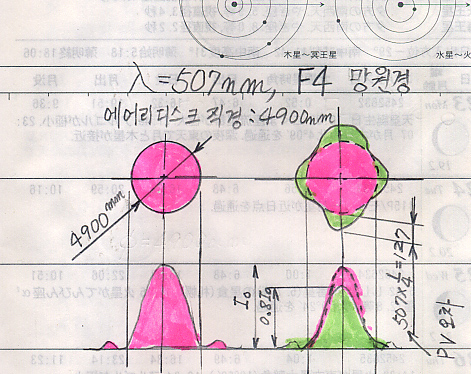
위의 그림을 보면 빛이 507나노메타이고 F4인 망원경에서 에어리디스크의 직경은 4900나노메타가 됩니다. 이 때 울퉁불퉁한 상점이 에어리디스크와 가장 차이나는 거리가 127나노메타였다면
파면 오차 = 127/507 = 1/4
즉 PV값은 1/4람다가 됩니다. 이 오차 한계가 레일리한계 분해능 각도를 볼 수 있는 한계 정밀도입니다. RMS값으로 기준하면 1/14람다 = 0.07람다 정도가 됩니다. 이 때의 광량을 본다면 레일리 원반 광량 피크치의 80%정도의 밝기가 됩니다.
이것이 이론적으로 오차를 허용할 수 있는 미러 정밀도의 한계치입니다. 이 정도면 충분하므로 1/4람다가 ‘미러의 한계허용정밀도’로 인용되고 실제 1/4람다이면 충분합니다. 문제는 실제로 메이커에서는 과장을 많이 하고 있어 그 수치를 완전히 신뢰할 수는 없다는 점입니다. 또 반사망원경의 경우는 사경의 회절도 고려해야하고, 에어리디스크의 크기는 사경값과 중첩되므로 좀 더 엄격한 미러의 경면정밀도를 요구하게 됩니다. 그렇더라도 1/8람다이면 충분할 것입니다. 단 실제로 1/8일 때 그렇습니다.
PS)
1. 원래 파면오차(wave front error)의 정의는 렌즈(미러)에서 굴절(반사)된 빛다발이 관측자가 사출동(射出瞳)에서 볼 수 있는 파면과 참조파면의 오차임에 유의해주세요.
2. 과거에 경면정밀도가 좋으면 좋을수록 좋다라는 의견이 많았습니다. 그러나 이론적으로 1/4람다 가공이면 레일리분해능 각도까지 충분히 관측할 수 있고, 대부분의 교재는 1/4람다를 최종 가공 미러라고 보고 데이터를 제시하고 있습니다.
3. 사진용 망원경이라면 1/4람다는 전혀 필요없습니다. 제가 사진을 찍어보니 1/2람다라도 충분하고도 남습니다. 시잉좋고 광축 잘 맞는게 좋고, 기구부가 튼튼한 제품이 좋습니다. 찍어보면 알아요~~
4. 저도 아마추어이므로 망원경의 모든 논리를 완벽하게 소화할 여력이 없고, 검증 받은 적도 없습니다. 위의 내용도 어디까지나 제 견해이므로 다른 의견 있는 분들은 리플글로 의견을 주시기 바랍니다.
 [re] 장시간 노출 사진과 안시에 대하여..
[re] 장시간 노출 사진과 안시에 대하여..
