촬영한 목성 사진 상의 특정 구조의 위도값을 구하는 일은 무척 귀찮긴 합니다만, 해외 커뮤니티에 정식으로 보고할 떄 단순히 '남적도대' '북적도대' 라 일컫는 방식보다 확실히 뭔가 있어 보이기도 하고, 실제로 목성 대기의 풍속을 계산하는 근간이 되므로 목성 관측기록의 기본이라 할 수 있겠습니다. 이 방면에 관심있으신 분이 또 계실까하여 예를 들어 적어보겠습니다.
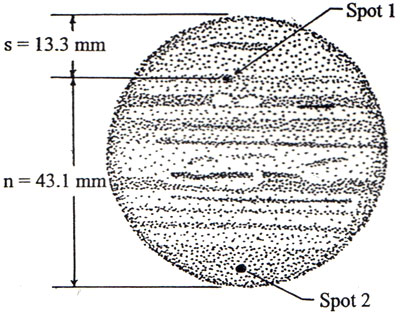
첨부한 그림은 1994년 7월 19일에 그려졌다고 하는 목성 스케치입니다만, 여기에서 Spot 1 의 위도값을 구해보려 합니다. 만일 목성이 완전한 구형이라면 Spot 1 의 위도(L)는 다음 식으로 손쉽게 얻을 수 있을 겁니다.
공식 1: 목성이 구형일 때의 가상의 위도(L)
Sin L = (s-n)/(s+n)
따라서, L = inv. Sin [(s-n)/(s+n)]
* inv. Sin 은 Sin 의 역함수로서 공학용 계산기를 통해 간단히 구해집니다.
그러나 실제 목성은 납작하게 짜부러져 있으므로 그에 맞추어 이 값을 수정해 줘야 합니다. 목성의 위도 체계에는 다음과 같이 Planetographic, Planetocentric, 그리고 Mean 이렇게 세 가지 종류가 있습니다.
공식 2-1: Planetographic
inv. Tan {1.0694 x Tan [inv. Sin (s-n)/(s+n) + 1.0694 D]}
공식 2-2: Planetocentric
inv. Tan {0.935 x Tan [inv. Sin (s-n)/(s+n)] + 1.0694 D]}
공식 2-3: Mean
inv. Sin (s-n)/(s+n) + 1.0694 D
여기에서 D 값은 목성 상에서 sub-Earth latitude 로서 관측 시기에 따라 달라지므로, 천문연감이나 calsky.com 등과 같은 온라인 툴 등에서 얻을 수 있습니다.
그럼 Spot 1 의 위도를 Planetographic 체계를 이용하여 구해 보겠습니다. 1994년 7월 19일의 sub-Earth latitude 를 뒤져보면 -3.41도 였다고 합니다. 또한 자를 이용해서 Spot 1 로부터 양극까지 떨어진 거리를 재 보았더니 남극과의 거리 s=13.3 mm, 북극과의 거리 n=43.1 mm 였습니다. 이들을 그대로 위 공식 2-1에 대입해 보면,
inv. Tan {1.0694 x Tan [inv. Sin (s-n)/(s+n) + 1.0694 D]}
= inv. Tan {1.0694 x Tan [inv. Sin (-0.5284) + 1.0694 x -3.41]}
= inv. Tan {1.0694 x Tan [-31.895 - 3.647]}
= inv. Tan {1.0694 x Tan [-35.542]}
= inv. Tan {1.0694 x -0.7144}
= inv. Tan {-0.7640}
= -37.38
마이너스 값이므로 남위 37.38도가 됩니다.
이번엔 마찬가지 방법으로 Spot2 의 위도를 구해 보겠습니다. Spot2의 남극과의 거리 s=52.4 mm, 북극과의 거리 n=4.0 mm 였고 마찬가지로 D= -3.41 이었다고 하면,
inv. Tan {1.0694 x Tan [inv. Sin (s-n)/(s+n) + 1.0694 D]}
= inv. Tan {1.0694 x Tan [inv. Sin (0.8582) + 1.0694 x -3.41]}
= inv. Tan {1.0694 x Tan [59.110 - 3.647]}
= inv. Tan {1.0694 x Tan [55.463]}
= inv. Tan {1.0694 x 1.4530}
= inv. Tan {1.5538}
= 57.2
즉 북위 57.2도가 됩니다.

 목성 대기 구조의 명명법
목성 대기 구조의 명명법
이런 자세한 방법등을 잘 알고 있어야 진정한 행성 관측가라고 할 수 있겠지요.
저는 취미로써 즐기기만 하는 경우라서....
하지만 더 많은 정보를 알려 주세요.^^