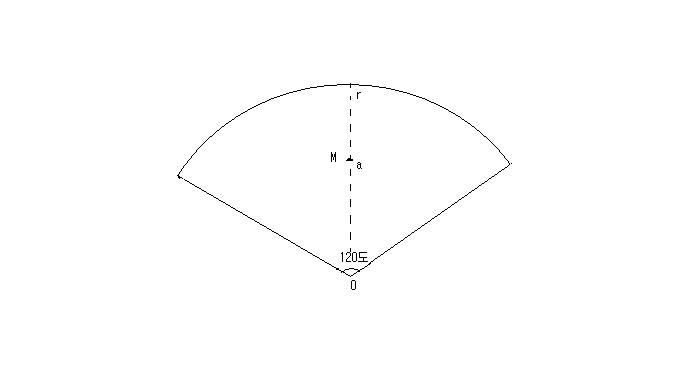
반경 r, 중심각 120도인 부채꼴 모양 조각 (즉, 원의 3등분 조각) 의 무게중심을 M이라고 하고,
(즉, M점을 받쳐주면 이 부채꼴은 쓰러지지 않고 균형을 잡을 수가 있겠습니다)
원의 중심 O로부터 부채꼴의 무게중심 M까지의 거리를 a라고 하면 a의 값은 얼마일까요?
물리적 moment의 총합이 제로가 되도록 약간의 적분을 이용하면
a = r * root(3) / π = 0.5513r
이 됩니다.
부채꼴이 아니고 삼각형이었다면 M은 2:1의 내분점이기 때문에 a= r * 2 / 3 =0.6667r 이 되겠지만 부채꼴인 경우는 원의 중심 쪽으로 좀 이동하는군요.
이 내용은 반사망원경 자작시 미러의 3점 지지, 또는 9점 지지에 이용될 수 있겠습니다.

 개기일식 연속촬영 2탄
개기일식 연속촬영 2탄