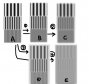
제가 본 이 그래프
황교수님 안녕하십니까.
제가 보기에는 이 그래프는 실험 그래프라 보여집니다. 이선생님 자료를 보니 18.4.5식 밑에 있는 글을 보면 줄 간격을 변경하면서 ‘측정’한다라고 적혀있습니다. 그 뿐만 아니라 이 실험을 근거로 나중에 육안관측결과도 나오지요.
무엇보다 이런 것을 실험하는 것은 별로 힘들지 않다는 점입니다. 어떻게 실험하는 방법은 언급을 하지않았지만 막상 보면 아주 쉽게 실험을 하는 경우가 많습니다. 또 수식이 시뮬레이션으로 보기에는 너무 원론적이고 간단합니다. 실제 시뮬레이션의 경우라면 이 설명을 할 때 변수를 많이 제시했을겁니다.
요즘 대부분 이런 정도는 대부분 시뮬레이션되었을겁니다만, 어느 시뮬레이션이던 많이 입력 변수가 많이 복잡하지요. 그래야 정확도가 올라가니까요. 예를들어 우리가 많이 사용하는 포토숍과 비슷한 것을 기업에도 제품 디자인에서 사용합니다. 그러나 비교가 되지않지요. 이건 색상의 양감, 질감을 다 나타낼 수 있을 뿐 아니라 그기서 바로 3D 화상 출력은 물론이고 유한요소법의 해석도 가능하도록 멀티화되었으니까요.
그리고 이 교재는 그냥 원론적인 내용을 적은 것으로, 개발자 전용의 전문서적은 아닌 것같습니다. 그렇다고 책 내용이 부실하다는 것이 아닙니다만 이 책에서 엄격한 것은 알 수없다는 이야기입니다. 또 초판출판도 제법 되지않았나 모르겠습니다. 학교, 기업에서 본격적인 시뮬레이션이 활성화된 것은 그리 오래되지 않습니다. 90년대 이후라고 봐야하고 이 책은 그전에 출판된 책이 아닌지 모르겠습니다.
무엇보다 시뮬레이션을 했던, 실험을 했던 이런 경향을 보이는 것은 맞다고 봐야지요. 그럼 그기에서 저는 제가 필요한 정보를 얻는 것이 제일 중요하다고 생각합니다.
................
그리고 종속변수, 독립변수 관계는 자연계에도 많이 있습니다. 예를들어 손으로 책상을 문지르면 열이 나는데 X축은 문지르는 속도, Y축은 발생열이라고 봅니다. X가 커지면 Y는 당연히 커지지만, Y가 커진다고 X가 커지지는 않습니다. 즉 열이 있다고 저절로 손이 책상에 문질러지지 않지요. 이것을 비가역과정이라고 하는데 자연계의 거의 대부분이 이런 과정입니다. 그렇지만 Y값을 보면 X값을 추정은 할 수있습니다.
이 그래프는 이런 것도 아니라고 봅니다. 극단적으로 그래프를 90도로 돌리면 Y축을 X축으로 하여 독립변수로 하여 실험을 해도, 실험이 번거로워서 그렇지 결과는 같이 얻을 수있습니다. 즉 그 CT를 변화시키면서 맺어지는 해상도를 측정하면 같은 결과가 얻어집니다. 물론 이때는 CT에 변화에 따라 해상도가 바로 나오는 시스템을 꾸며야겠지요.
>예 맞습니다. 이 그래프로 본다면 중앙차폐가 있는게 낫습니다. 그러나 이 그래프는 F10인 경우에 한하므로 다른 F수에는 좀 변동이 있을겁니다. 그렇더라도 큰 변동은 없을겁니다. 그러니 딥스카이에서는 비슷하다고 봐야겠지요. 그런데 이건 어찌보면 너무나 당연한 이야기입니다. 초고감도 ccd를 사용하면 광량이라는 변수가 떨어져나갑니다. 그럼 구경인데 구경은 커되 광량이 많이 들어올 필요가 없습니다. 괜히 씰데없는 빛들이 많이 들어와서 분란만 칠 것이므로 소수의 똑똑한 빛들만 오는게 사진화질에 더 낫지않겠습니까. 말되남요?
>...........................
>
>이왕하는 말하는 것, 마지막 마무리를 해야겠습니다. 이제 요위의 그림의 주석 내용이 그렇게 이상하게 안보이시리라 생각합니다. 제가 좀 비약을 해서 적었는지 모르겠군요.
>
>1. 이 연구자는 1/4람다를 최종 미러라 생각하고 참고용으로 실험했습니다. 안그러면 그 위의 미러를 가지고 실험을 했겠지요.
>
>2. 붉은 선의 끝부분은 천문년감의 표에 나오는 값과 거의 비슷합니다. 즉 실험을 줄이기 위해 마지막에는 직선을 그었습니다.
>
>3. 실험용 미러는 람다 표시가 없는걸보아 일반미러를 가지고 실험을 했지싶습니다. 그래도 해상력, 차폐실험에 문제가 없습니다. 1/4람다 미러는 미러집에 가서 담뱃값주고 빌려와서 실험을 했을겁니다.
>
>마지막으로 제일 위의 식을 봐 주십시요. 이것이 필름(or ccd)과 그 망원경이 합쳐졌을 때 내는 최종 해상력 식입니다. 망원경 해상력이 나왔지만 필름도 고유 해상력이 있습니다. 제가 옥이방 창살은 고정되어 있다는 말을 계속한 것은 이것 때문이었습니다. 여기서 망원경 최대해상력(고유해상력)과 필름 최대(고유해상력)의 역수를 합한 것이 천체해상력의 역수입니다. 여기서 중요한 것은 같은 필름도 망원경의 F수에 따라서 해상력이 변하면서 대응한다는 것입니다. 왜 그렇느냐하면 초점면의 밝기가 망원경 F수에 따라 변하니까 그렇습니다.
>...........................
>
>이제 마무리입니다. 제가 1번글에서 분해능, 해상력, 콘트라스트는 경면정도와 전혀 관계가 없다고 했습니다. 이 때는 이만성선생님 자료를 보기도 전이었습니다. 사실 보다싶이 관계가 없습니다.
>
>........................
>경면정밀도
>이건 망원경 구면수차에만 관계됩니다. 그러나 이것이 망원경 화질에 영향을 끼치는 부분이 많다고 보여집니다. 천문인들이 경면정밀도, 정밀도하는게 일리가 있을거든요. 참 사람눈이 예민한 것같습니다.
>
>그러나 경면정밀도를 측정하는 방법과 여러 홈페이지에 가끔씩 인용되는 자료에 대해서는 별 관심이없어서 잘모르겠습니다. 참고로 1/4람다는 5500/4 = 약 1400옹스트롬이고 1/8람다는 700옹스트롬입니다. 물분자 크기가 3.4옹스트롬이고 석유분자들이 대략 4옹스트롬이 나옵니다. 그럼 1/8람다는 석유분자의 약 100배크기입니다. 여러분! 분자 크기가 얼마나 작은지 아시나요?
>
>틀림없는 것은 레일리한계는 ‘기하공차 1/4람다’이고 기하공차를 측정하는 것은 아주 따분하고 시간이 많이 걸리는 작업이라는 것입니다. 혹시 아시는 분중에 렌즈 연마 제작 관련 업종에 근무하시는 분들이 있으면 한번 문의해보시면 잘 아실겁니다.
>
>이상 마칩니다.
>
>
황교수님 안녕하십니까.
제가 보기에는 이 그래프는 실험 그래프라 보여집니다. 이선생님 자료를 보니 18.4.5식 밑에 있는 글을 보면 줄 간격을 변경하면서 ‘측정’한다라고 적혀있습니다. 그 뿐만 아니라 이 실험을 근거로 나중에 육안관측결과도 나오지요.
무엇보다 이런 것을 실험하는 것은 별로 힘들지 않다는 점입니다. 어떻게 실험하는 방법은 언급을 하지않았지만 막상 보면 아주 쉽게 실험을 하는 경우가 많습니다. 또 수식이 시뮬레이션으로 보기에는 너무 원론적이고 간단합니다. 실제 시뮬레이션의 경우라면 이 설명을 할 때 변수를 많이 제시했을겁니다.
요즘 대부분 이런 정도는 대부분 시뮬레이션되었을겁니다만, 어느 시뮬레이션이던 많이 입력 변수가 많이 복잡하지요. 그래야 정확도가 올라가니까요. 예를들어 우리가 많이 사용하는 포토숍과 비슷한 것을 기업에도 제품 디자인에서 사용합니다. 그러나 비교가 되지않지요. 이건 색상의 양감, 질감을 다 나타낼 수 있을 뿐 아니라 그기서 바로 3D 화상 출력은 물론이고 유한요소법의 해석도 가능하도록 멀티화되었으니까요.
그리고 이 교재는 그냥 원론적인 내용을 적은 것으로, 개발자 전용의 전문서적은 아닌 것같습니다. 그렇다고 책 내용이 부실하다는 것이 아닙니다만 이 책에서 엄격한 것은 알 수없다는 이야기입니다. 또 초판출판도 제법 되지않았나 모르겠습니다. 학교, 기업에서 본격적인 시뮬레이션이 활성화된 것은 그리 오래되지 않습니다. 90년대 이후라고 봐야하고 이 책은 그전에 출판된 책이 아닌지 모르겠습니다.
무엇보다 시뮬레이션을 했던, 실험을 했던 이런 경향을 보이는 것은 맞다고 봐야지요. 그럼 그기에서 저는 제가 필요한 정보를 얻는 것이 제일 중요하다고 생각합니다.
................
그리고 종속변수, 독립변수 관계는 자연계에도 많이 있습니다. 예를들어 손으로 책상을 문지르면 열이 나는데 X축은 문지르는 속도, Y축은 발생열이라고 봅니다. X가 커지면 Y는 당연히 커지지만, Y가 커진다고 X가 커지지는 않습니다. 즉 열이 있다고 저절로 손이 책상에 문질러지지 않지요. 이것을 비가역과정이라고 하는데 자연계의 거의 대부분이 이런 과정입니다. 그렇지만 Y값을 보면 X값을 추정은 할 수있습니다.
이 그래프는 이런 것도 아니라고 봅니다. 극단적으로 그래프를 90도로 돌리면 Y축을 X축으로 하여 독립변수로 하여 실험을 해도, 실험이 번거로워서 그렇지 결과는 같이 얻을 수있습니다. 즉 그 CT를 변화시키면서 맺어지는 해상도를 측정하면 같은 결과가 얻어집니다. 물론 이때는 CT에 변화에 따라 해상도가 바로 나오는 시스템을 꾸며야겠지요.
>예 맞습니다. 이 그래프로 본다면 중앙차폐가 있는게 낫습니다. 그러나 이 그래프는 F10인 경우에 한하므로 다른 F수에는 좀 변동이 있을겁니다. 그렇더라도 큰 변동은 없을겁니다. 그러니 딥스카이에서는 비슷하다고 봐야겠지요. 그런데 이건 어찌보면 너무나 당연한 이야기입니다. 초고감도 ccd를 사용하면 광량이라는 변수가 떨어져나갑니다. 그럼 구경인데 구경은 커되 광량이 많이 들어올 필요가 없습니다. 괜히 씰데없는 빛들이 많이 들어와서 분란만 칠 것이므로 소수의 똑똑한 빛들만 오는게 사진화질에 더 낫지않겠습니까. 말되남요?
>...........................
>
>이왕하는 말하는 것, 마지막 마무리를 해야겠습니다. 이제 요위의 그림의 주석 내용이 그렇게 이상하게 안보이시리라 생각합니다. 제가 좀 비약을 해서 적었는지 모르겠군요.
>
>1. 이 연구자는 1/4람다를 최종 미러라 생각하고 참고용으로 실험했습니다. 안그러면 그 위의 미러를 가지고 실험을 했겠지요.
>
>2. 붉은 선의 끝부분은 천문년감의 표에 나오는 값과 거의 비슷합니다. 즉 실험을 줄이기 위해 마지막에는 직선을 그었습니다.
>
>3. 실험용 미러는 람다 표시가 없는걸보아 일반미러를 가지고 실험을 했지싶습니다. 그래도 해상력, 차폐실험에 문제가 없습니다. 1/4람다 미러는 미러집에 가서 담뱃값주고 빌려와서 실험을 했을겁니다.
>
>마지막으로 제일 위의 식을 봐 주십시요. 이것이 필름(or ccd)과 그 망원경이 합쳐졌을 때 내는 최종 해상력 식입니다. 망원경 해상력이 나왔지만 필름도 고유 해상력이 있습니다. 제가 옥이방 창살은 고정되어 있다는 말을 계속한 것은 이것 때문이었습니다. 여기서 망원경 최대해상력(고유해상력)과 필름 최대(고유해상력)의 역수를 합한 것이 천체해상력의 역수입니다. 여기서 중요한 것은 같은 필름도 망원경의 F수에 따라서 해상력이 변하면서 대응한다는 것입니다. 왜 그렇느냐하면 초점면의 밝기가 망원경 F수에 따라 변하니까 그렇습니다.
>...........................
>
>이제 마무리입니다. 제가 1번글에서 분해능, 해상력, 콘트라스트는 경면정도와 전혀 관계가 없다고 했습니다. 이 때는 이만성선생님 자료를 보기도 전이었습니다. 사실 보다싶이 관계가 없습니다.
>
>........................
>경면정밀도
>이건 망원경 구면수차에만 관계됩니다. 그러나 이것이 망원경 화질에 영향을 끼치는 부분이 많다고 보여집니다. 천문인들이 경면정밀도, 정밀도하는게 일리가 있을거든요. 참 사람눈이 예민한 것같습니다.
>
>그러나 경면정밀도를 측정하는 방법과 여러 홈페이지에 가끔씩 인용되는 자료에 대해서는 별 관심이없어서 잘모르겠습니다. 참고로 1/4람다는 5500/4 = 약 1400옹스트롬이고 1/8람다는 700옹스트롬입니다. 물분자 크기가 3.4옹스트롬이고 석유분자들이 대략 4옹스트롬이 나옵니다. 그럼 1/8람다는 석유분자의 약 100배크기입니다. 여러분! 분자 크기가 얼마나 작은지 아시나요?
>
>틀림없는 것은 레일리한계는 ‘기하공차 1/4람다’이고 기하공차를 측정하는 것은 아주 따분하고 시간이 많이 걸리는 작업이라는 것입니다. 혹시 아시는 분중에 렌즈 연마 제작 관련 업종에 근무하시는 분들이 있으면 한번 문의해보시면 잘 아실겁니다.
>
>이상 마칩니다.
>
>
 전체 해상도 보조 설명
전체 해상도 보조 설명