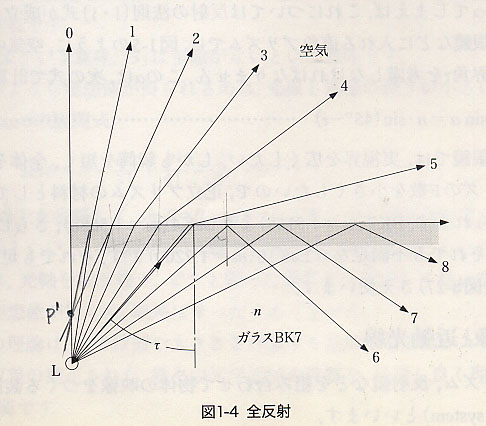
예, 위의 내용은 수직선 근처의 굴절 빛을 그린 것입니다. 그러나 그림이 너무 실제 상황과 달라서 다시 다른 그림을 올립니다. 위 그림은 실제 캐드로 정확하게 그린 것을 축소한 그림입니다.
위의 그림에서 전등 L의 불빛은 물속에서 여러 방향으로 퍼져나갑니다. 위 그림대로 1번에서 8번 방향과 같이 퍼져나갑니다.
제가 말하고자 하고자하는 것은 수직선과 미소각도 떨어진 1번 불빛인데요. 이 불빛과 미소 각도로 떨어져 있는 1‘ 불빛이 있다면 1과 1’의 연장선상의 교점이 떠보이는 불빛 P'가 되지싶습니다. 윗그림에서는 1‘가 없으므로 2번 불빛으로 그대로 연장선상을 그어보았습니다. 이 점이 떠 보이기 상 위치라고 생각합니다.
그런데 황교수님 지적처럼 1과 1‘가 수직선상에 있을 것이냐는 것은 굴절율과 광선 위치에 관계됩니다. 물의 굴절율은 1.33이므로 그 비율만큼 꺾어지는데 엄밀히 말해서 1불빛이 수직선상에 접근할 때까지는 떠보이는 동전이 수직선상에 있을 수는 없습니다. 딱 한점에 모일려면 굴절율이 1이 될 수 밖에 없으니까요.
그러나 광선 1이 수직선과 미소각도 떨어진 광선이라면 1과 1‘의 교점은 수직선상의 거의 P'에 위치하게 됩니다(극한치 개념임) 이 때 수직선상에서 보았을 때 P'위치(깊이 h')는 깊이 h를 굴절율로 나눈 값과 같다는 이야기입니다.
수직선과 떨어진 광선은 h'가 h/n이 될 수 없습니다. 4, 5번 광선을 생각해보면 되는데, 미소각도 떨어진 4’와 5‘를 광선을 연장시켰을 때는 수직선과 한참 떨어진 위치에 상이 맺어진다는 것을 알 수있습니다.
그러므로 먼저 손으로 그림은 수직선과 미소각도 떨어진 광선입니다. 그림이 좀 황당해서 그렇지요.
만약 윗그림에서 눈을 4나 5위치에서 동전을 본다면 동전은 수면 바로 아래쪽까지 떠 보이리라 생각합니다. 4, 5 광선과 미속각도로 떨어진 4‘, 5’를 생각하여 연장선을 그으면 그렇습니다. 물론 이 동전 위치는 수직선과 한참 떨어진 위치에서 보이겠지요(더 얕게 보이면서, 눈 쪽으로 치우쳐 보이겠지요).
바로 수직선상에서 동전이 상을 작도하는 것은 아이디어가 안떠오르는군요. 나중에 모임 때 연필과 종이 들고 가겠습니다.
여기까지가 제 생각입니다.
 물속의 동전 깊이 작도(황교수님 숙제)
물속의 동전 깊이 작도(황교수님 숙제)