안녕하세요
마침 제가 가진책 JENKINS/WHITE 의 Fundamentals of Optics 에 그 식을 유도한 부분과 그림이 있어서 올려봅니다.
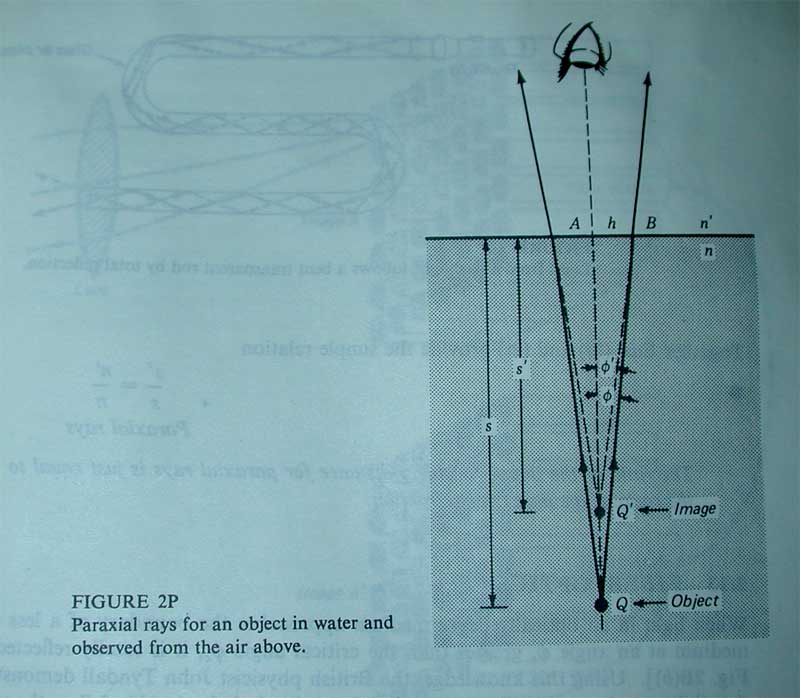
제목은 'Paraxial Rays 에 의해 형성된 이미지' 입니다.
제가 가진 사전에는 Paraxial 이란 단어는 없는데 거의 축과 다름이 없는 즉 보통 x, y 좌표계에서 y 축과 거의 벗어나지 않는 rays 를 이용한 방법 같습니다.
번역이 어떨지는 몰라도 책의 내용을 보면
많은 관측자들에게 특히 관심이 있는 것들이 작은 각 φ와 φ' 를 이루는 광선들에 있어서 물체와 이미지의 거리 s 와 s' 입니다.
이탤릭체로
코사인이 1과 같고 싸인과 탄젠트가 그 각과 같은 장치 설치가 허용되는 충분히 작은 각을 이루는 광선들을 paraxial rays 라고한다.
직각 삼각형 QAB 와 Q'AB 를 볼때
h=s tan φ=s' tan φ'
s'=s (곱하기)tanφ/tanφ' = s(곱하기) sinφcosφ'/cosφsinφ'
여기에 Snell 의 법칙
sinφ/sinφ' = n'/n ---------------(1)
을 적용하면
윗식은 s' = s(곱하기)n'/n(곱하기)cosφ'/cosφ 가 됩니다.
Paraxial rays 에서 각 φ 와 φ' 은 매우 작으므로 윗식은
s'=s(곱하기)φ/φ' 또는 s'/s = φ/φ' -------(2) 로 쓸수 있습니다.
(1) 식과 (2)식으로부터 s'/s=n'/n 이 됩니다.
여기에서 n' 은 바깥쪽의 굴절률 입니다.
이탤릭체로
Paraxial rays 에 있어서 이미지와 물체거리의 비율은 바로 굴절지수의 비율과 같다.
이상입니다. 안녕히 계세요.

 [re] 물속 동전 떠 보이기 깊이 재정리
[re] 물속 동전 떠 보이기 깊이 재정리
 궁금합니다...
궁금합니다...